Schrödinger's Wave Equation
We introduced you to the wave-like nature of matter particles, or matter waves, in Chapter 5. Erwin Schrödinger, an exceptionally gifted Austrian physicist, explored the consequences of these matter waves and proposed a wave equation for them, analogous to the known equations for other wave motions in nature. This wave equation describes how a wave associated with an electron or other subatomic particle varies in space and time as the particle moves under various forces.
Schrödinger's theory of the quantum world is called wave mechanics. He worked out the exact solutions of the wave equation for the hydrogen atom, and the results perfectly agreed with the known energy levels of these atoms, seemingly without any of the complications and metaphysical speculations associated with the uncertainty principle. Moreover, the equation could also be applied to more complicated atoms, and even to particles not bound in atoms at all. It was soon found that in every case, Schrödinger's equation gave a correct description of a particle's behaviour, provided it was not moving at a speed near that of light. [1]
In spite of this success, the very meaning of the waves remained unclear. Schrödinger believed that the intensity of the wave at a point in space represented the 'amount' of the electron that was present at that point. In other words, the electron was spread out, rather than concentrated at a point. However, it was soon found that this interpretation was untenable, because observations revealed that particles never spread out. For example, it follows from the wave equation that when a wave, representing an electron, strikes a target, it spreads out in all directions. Experimentally, on the other hand, the electron scatters in some specific direction but never breaks up.
Max Born's Interpretation of the Wave Equation

Max Born, another German physicist and a good friend of Einstein, interpreted this result as follows: the wave associated with the electron is not a tangible 'matter wave', but one that determines the probability of scattering of the electron in different directions. Where the associated wave has a large amplitude, the probability of finding an electron there is high. In any case, one would find the whole particle, and not parts of it.
This indicated that the simple interpretation of the wave equation as a description of the physical matter waves in ordinary space, as was originally assumed by Schrödinger himself, is incorrect. Born noted the following conclusions:
- Matter waves represent probability amplitudes associated with the occurrence of an event.
- If there are multiple alternatives for the event to happen, the total amplitude is the sum of the alternative amplitudes.
- Finally, the absolute square of the overall amplitude, the intensity of the wave, must be interpreted as the probability that the event will happen.
This difference between the world of the very small and the everyday world we experience cannot be understated. When you are walking across a street and an automobile is approaching you, it is at a definite place at any given time, and it is possible to describe with a great deal of precision where exactly the automobile is, and where it will be at another moment in time if it continues on the same path. For objects in the realm of the very small, this is simply not possible.
These discoveries are at the heart of quantum physics. The importance of the introduction of statistical probabilities into physical law cannot be understated. In earlier physics, that is to say the classical mechanics of Isaac Newton, probabilities had no place. In the Newtonian world-view, an object of any kind could at least in theory be described as having a definite position at any given time. This was not the case at all in the new quantum theory: the probabilities describing material particles could never be replaced by old-style definite positions.
A Probabilistic World
Applying these points to an electron in an atom, nevertheless, we see that the electron is no longer a point in space moving along a definite path, but a cloud of probabilities [2]. In other words, one cannot say that an electron will be in this position at this point of time, but one can only say like this: 'It is 95% probable that the electron will be at this position at this point of time.' Similarly, to every point in a light wave we can attach a numerical probability (per unit time interval) that a photon can be detected in any small volume centred on that point, and light is viewed as a probability wave.
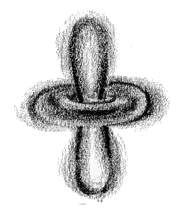
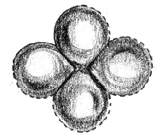
Fig. 7-1: Electron probability clouds for the s-, p- and
d-orbitals *
With de Broglie's principle, we can also extend this to electrons and all other matter particles, and hence account for their wave nature (and hence the double-slit experiment). They have been experimentally found to be correct; in 1994, interference fringes, a typical characteristic of waves, were generated with beams of iodine molecules, which are about 500,000 times more massive than electrons.
By 1930s, this indeterministic interpretation of quantum physics, mainly put forward by Niels Bohr with support from Born's probability interpretation and Heisenberg's uncertainty principle, came to be known as the Copenhagen interpretation, mainly because Bohr ran an influential physics institute there during this period. What happened next is dealt with in the next chapter.
Footnotes
1. At speeds comparable to that of light, particles begin to behave strangely. That, however, is a part of the relativity theory, and we shall not touch upon the matter. Back2. It is impossible to give an everyday world analogy for this 'cloud of probabilities'. Nevertheless, this is the best description of how these particles exist and behave. Back
* Fig. 7-1 Courtesy: Creation Explanation